Prospect Theory is one of the most famous behavioral finance theory. It describes how investors make decisions under risk and how we can predict their risk profile.
A short introduction to this theory is given in this article.
Let’s imagine you can invest in a bet with a 50% chance of getting either $100 or $0, or get $50 directly. What do you prefer?
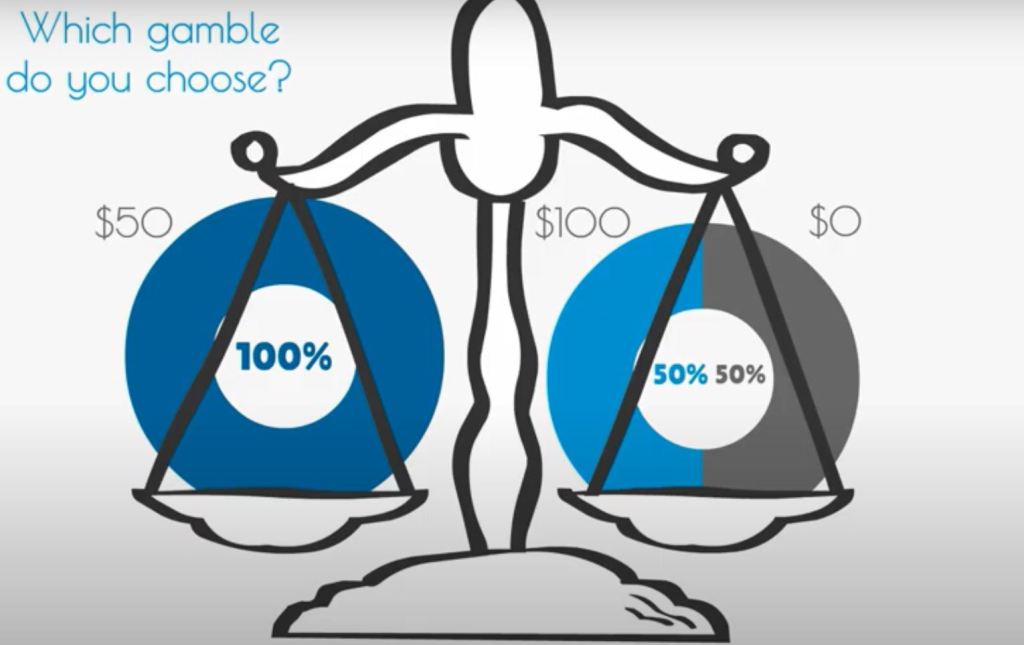
Based on traditional financial theories, a “rational” and risk-neutral investor should calculate the average/mean or expected value (EV) of the bet and invests only if the EV is greater than the price of the bet.
In our example, this investment strategy means that a rational investor will accept to play the gamble if the alternative is $50 or less ($100X50% + $0X50% = $50).
However, most investors are much more risk-averse than theoretical “rational” agents.
Sensitivity to gains
Based on economic experiments, a large majority of investors prefer to take the $50 rather than gambling. They prefer also to get $40, or even for some of them $30, rather than taking the risk of getting nothing.
Moreover, the higher the outcome, the less sensitive investors become to an increase in this outcome. We will appreciate to get a $10 free gift coupon rather than nothing. However, winning $11k at a casino instead of $10k does not make a real difference.
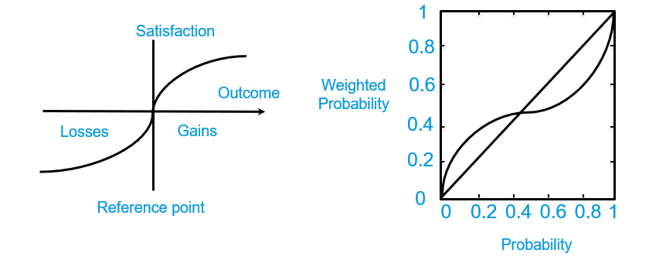
To account for this first psychological parameter (gain sensitivity), we can say that the utility we attribute to financial gains is often concave. We underestimate large gains and are much more sensitive to an increase in small gains than in large gains.
Loss aversion
Now, what if I asked you to choose between paying $50, and placing a bet where you have 50% chance of paying either $100 or nothing?
In this case, most of us prefer to gamble. There is some hope not to lose. We try our chances. Even for $25, we may be ready to gamble.
Most of us are afraid of losing. On average, economic experiments show we are twice more sensitive to losses than to gains.
Moreover, we are much more sensitive to a change in small losses than in big losses. If we expect to pay $10 for your meal and get a $20 bill, we become quite upset.
If we buy a house $1.01M instead of $1M, it may not really matter.
In a nutshell, our valuation of losses is often convex.
Loss aversion is one of the most fundamental heuristics in our financial decisions. It is also present among very young children and capuchin monkeys (Chen, 2006). We can speculate that this makes sense from an evolutionary point of views. Our hot-headed and fearless ancestor may not have survived long in the savannah…
Probability distortion
Finally, you may not care about buying a pill with a 90% or 90.5% chance of success. But you may strongly prefer a 100% safe pill over a pill with a 0.5% risk.
To sum things up, we tend to distort probabilities. Small probabilities are overweighted. Large probabilities are underweighted. 30% is most of the time the limit.
We are also more or less optimist or confident in our financial decisions. If you drive a car for the first time and are told that 1M+ people die each year on the road, you may be quite scared and over weigh the probability of crashing. If you are an experienced driver, you may on the contrary be overconfident and under weigh the risk.
Prospect Theory is a decision-making model under risk which takes into account all these psychological factors. Developed by the Nobel Prize winners Daniel Kahneman and Amos Tversky in 1979, Prospect Theory is at the heart of behavioral finance (Kahneman & Tversky, 1979; Wakker, 2011).
Prospect Theory
Let’s take a bet, L, that pays x with a probability of either p or y. x and y can be positive or negative.
How do people value this bet?
As discussed above, the mathematical average/mean o Expected Value does not take into account personal preferences and cognitive bias.
We assume that each person has a unique value function U to evaluate the bet L:
U(L) = w(p)u(x) + (1 −w(p))u(y)
With u the utility function:
u(x) = xα, x > 0,
u(x) = − λ( − x)α, x < 0 α is the concavity/convexity or “Greed” parameter. λ is the loss aversion or “Fear” parameter.
w is the probability weighting function with two parameters: w(p) = (exp( − ( − ln p)σ))β with β>0 the elevation/pessimism parameter and σ>0 the curvature/likelihood insensitivity parameter. If 0<β<1, the probability weighting function captures optimism. If β > 1 the probability weighting function captures pessimism. If 0<σ<1, the function reflects inverse s-shape pattern where small probabilities are over weighed and large probabilities are under weighed.
Contrary to the classical framework, there is not one specific parameter for risk-taking in Prospect Theory.
Risk tolerance results from the combination of loss aversion, concavity of the utility function, and pessimism and likelihood insensitivity of the probability function.
Most empirical studies show that we tend to exhibit a fourfold pattern with risk-aversion for large probabilities and risk-seeking for small probabilities in the gain domain, risk-aversion for small probabilities and risk-seeking for large-probabilities in the loss domain.
There is however a high variability at the level of the individual.

