Si un test visant à détecter une maladie dont la prévalence est de 1/1000 a un taux de faux positifs de 5 %, quelle est la probabilité qu’une personne dont le résultat est positif soit réellement atteinte de la maladie, en supposant que vous ne connaissiez rien des symptômes de cette personne ?
Cette question a été posée à 60 étudiants en médecine de Harvard en 1978 par Schoemberger, Grayboys and Casscells.
La moyenne des réponses des élèves était de 0,95… alors que la réponse correcte est de 0,02.
Que s’est-il passé ?
L’erreur du taux de base est une erreur, un biais cognitif, qui se produit lorsque la probabilité conditionnelle de l’évènement A sachant qu’un évènement B est réalisé est calculée en ignorant l’évènement B en question.
En ce sens, ce biais cognitif nous empêche de suivre le théorème de Bayes. Un concept un technique et pas toujours intuitif que nous nous efforçons ci-dessous d’expliquer.
Pour rappel, le théorème de Bayes stipule :
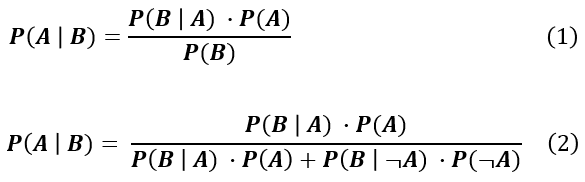
Dans notre exemple disons que :
- D représente « le patient a la maladie » et P(D) représente la probabilité de l’évènement « le patient a la maladie ». Cette probabilité est de 1/100.
- D_ représente l’évènement « le patient n’a pas la maladie ». La probabilité est P(D_) est de 1-1/100=0,999.
- P représente l’évènement « le test est positif ».
- P(D/P) est la probabilité que le patient ait la maladie, sachant que le patient a un test positive. C’est ce qu’on veut calculer.
- P(P/D) est la probabilité que le test soit positif, sachant que le patient a la maladie.
- P(P/D_) est la probabilité que le test soit positif sachant que le patient n’est pas malade. Cette probabilité est de 0,05.
Ce que les personnes font : ils ignorent la probabilité antérieure de la maladie. Le test est faux dans 5% des cas. Cela signifie que si le test est positif, dans 5% des cas, il est faux. Ainsi, la probabilité d’avoir un test positif et d’avoir réellement la maladie est de 95 %.
Dans leur tête, P(D/P) est équivalent à 1-P(P/D_).
Réponse correcte (basée sur le Théorème de Bayes):
La probabilité d’avoir la maladie, sachant que le test est positif est pourtant :
P(D/P)=P(D)*P(P/D)/P(P)= P(D)*P(P/D)/(P(D)*P(P/D)+ P(D_)*P(P/D_)))
=0,001*1/(0,001*1+0,05*0,999)
=2%
Ce biais affecte beaucoup de nos décisions d’investissement.
Lorsqu’on lit la description d’un produit financier, par exemple, nous avons tendance à nous concentrer sur les performances passées afin d’avoir une idée des performances futures.
L’oubli de la fréquence de base peut également expliquer le biais du survivant, où l’on interprète la bonne performance des fonds sans tenir compte des résultats de ceux qui ont disparu.
Référence :
Gigerenzer, G. (1993). The bounded rationality of probabilistic mental models. In This chapter is based on a lecture delivered at Harvard University, Oct 2, 1991.. Taylor & Frances/Routledge.

